
A TI-84 or N-Spire CX CAS calculator is required for this course. Lastly, students should be able to develop an appreciation of calculus as a coherent body of knowledge and as a human accomplishment. Furthermore, they should be able to determine the reasonableness of solutions, including sign, size, relative accuracy, and units of measurement. (b) Write an equation for the position, x (t. t (a) Write an equation for the velocity, v (t), of the particle for all t > 0. When t 1, the position of the particle is 6 and the velocity is 2. Students should be able to model a written description of a physical situation with a function, a differential equation, or an integral and they should be able to use technology to help solve problems, experiment, interpret results, and verify conclusions. A particle moves along the x-axis in such a way that its acceleration at time t for t > 0 is 3 given by: a ( t ) 2. In addition, students should be able to communicate mathematics both orally and in well-written sentences and be able to explain solutions to problems. They should also comprehend the relationship between the derivative and the definite integral as expressed in both parts of the Fundamental Theorem of Calculus. Students should be able to understand the meaning of the definite integral, both as a limit of Riemann sums and as the net accumulation of change, and should be able to use integrals to solve a variety of problems. Students will be familiar with the meaning of the derivative in terms of a rate of change and local linear approximation and be able to use derivatives to solve a variety of problems. According to the College Board, students should be able to work with functions represented in a variety of ways: graphical, numerical, analytical, or verbal, and understand the connections among these representations. The course is based on the four major concepts of calculus: limits, derivatives, definite and indefinite integrals. Students can use graphing calculators on both AB and BC exams.AP Calculus AB is a full-year, college level course in the calculus of functions of one independent variable.

Additionally, students should be able to identify and apply appropriate calculus concepts to real-world problems and communicate their solutions effectively using mathematical notation and language. They should also be able to read and interpret complex graphs, understand mathematical notation, and solve problems using various methods. To succeed in the AP Calculus BC exam, students should have a strong foundation in algebra, geometry, trigonometry, and single-variable calculus. Students are expected to have a solid understanding of these topics and the ability to apply calculus concepts to solve problems. The exam covers limits and continuity, derivatives, integrals, applications of derivatives and integrals, differential equations, parametric equations and polar coordinates, infinite sequences and series, and vector calculus. The free-response section consists of 6 questions and students have 1 hour and 30 minutes to complete it. The multiple-choice section consists of 45 questions and students have 1 hour and 45 minutes to complete it. This exam is split into multiple-choice and free-response. They should also be able to read and interpret graphs, understand mathematical notation, and solve problems using various methods. To succeed in this exam, students should have a strong foundation in algebra, geometry, and trigonometry, as these concepts are fundamental to calculus. The exam covers limits and continuity, derivatives, integrals, applications of derivatives and integrals, and differential equations.
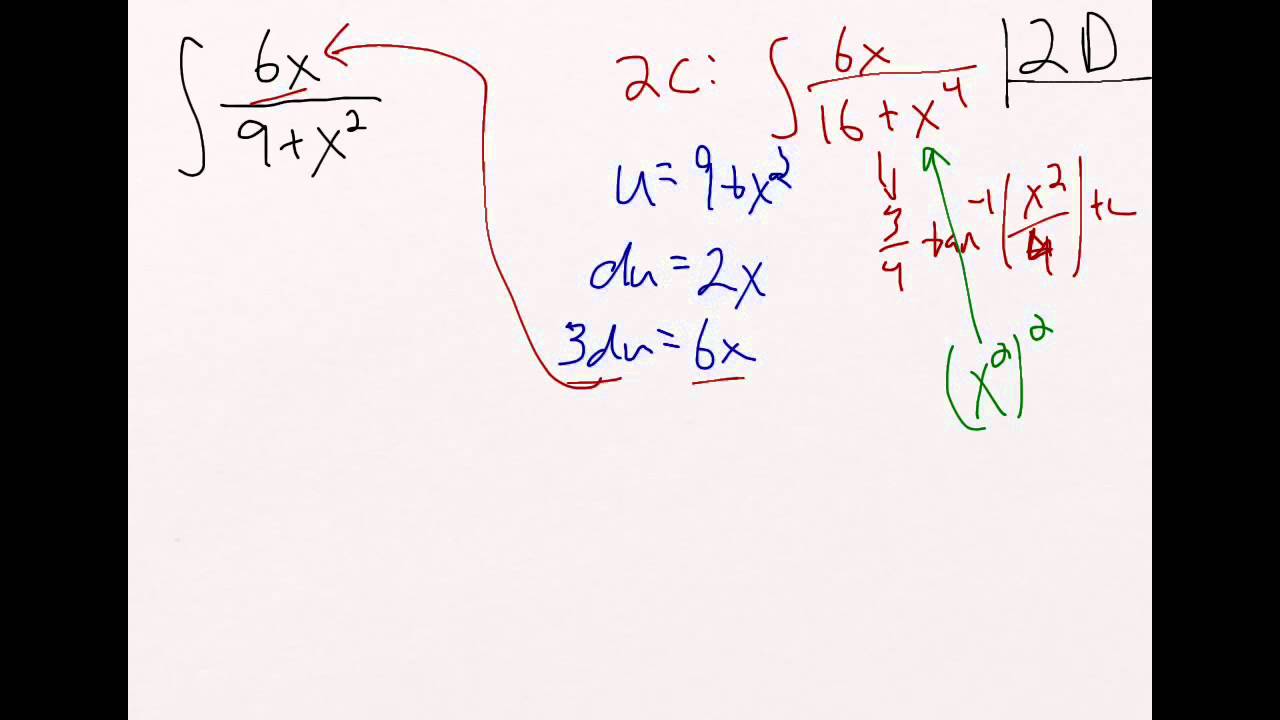
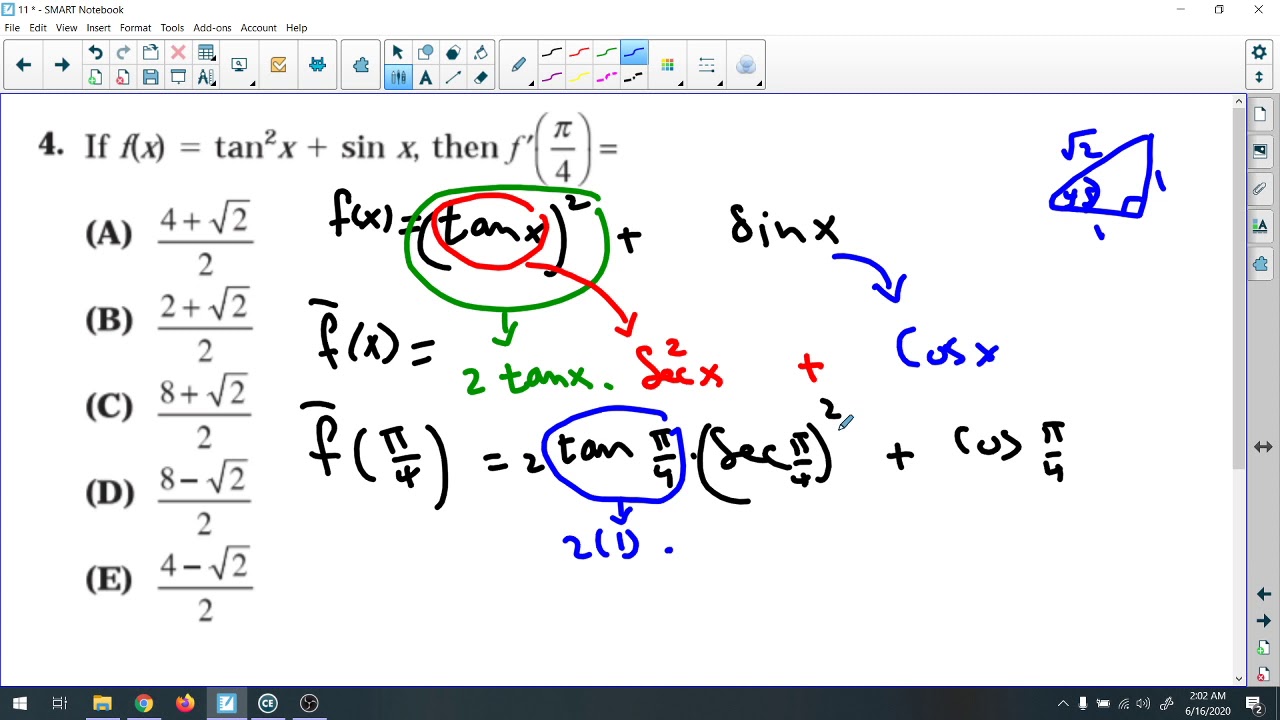
#Calc ab free
The free response section consists of 6 questions and students have 1 hour and 30 minutes to complete it. The multiple choice section consists of 45 questions and students have 1 hour and 45 minutes to complete it. The exam is split into two sections: multiple choice and free response.


 0 kommentar(er)
0 kommentar(er)
